The heart of Einstein's theory of gravity is the curved spacetime. It accounts for why apples fall towards the earth, why clocks slow down near massive bodies, and how galaxies can move apart faster than the velocity of light although the galaxies are at rest! To visualize the curved spacetime is however not so easy. We need to make some kind of translation from the full theory to illustrate the curved spacetime with for instance a curved surface.

The technique used here gives images that requires a bit more knowledge to interprete correctly than those of spacetime1. On the other hand, when interpreted correctly, all the features of the true spacetime of a line will be incorporated. Also some of the more important features - like why clocks near massive objects run more slowly relative to clocks further from the massive object - can be explained without any background knowledge. The explanation below is currently very brief, and mainly intended for those who have already been introduced to this way of explaining.

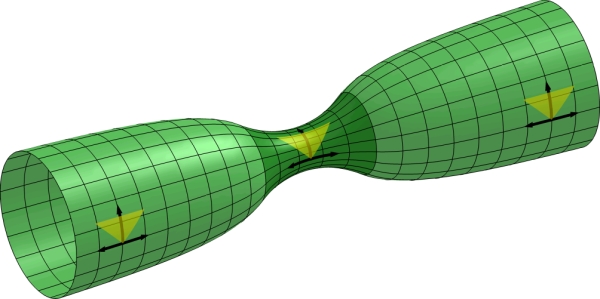
The spacetime of a line through a very dense planet

Imagine that we drill a large hole through a very dense planet. Through this hole we put a long staff - extending on both sides of the planet, from left to right. The spacetime of this line may be depicted as the hourglass-shaped surface below.

Time from geometry

From the surface we can easily read off distances and times as experienced by an observer at rest. One centimeter around the surface (as opposed to along the surface) corresponds to one unit of time (say one second). One centimeter along the surface corresponds to one length unit (say 1 cm). Already now we may see that there is less time experienced per lap in the center of the spacetime than in the outskirts. There is a simply shorter distance per lap in the center than in the outskirts - hence shorter time. Indeed time runs slow inside the planet relative to the outside. Below follows a more strict argument. Notice incidentally that the surface should not be closed in the time direction, rather after one lap around the spacetime we should be on a new layer - like on a toilet roll.

An experiment with photons

Suppose that the distance per lap around the spacetime is 10 seconds to the far left, and 5 seconds around the center dip. Now let a person on the outside send two photons, 10 seconds apart, towards the center of the planet where another person receives the photons. On the spacetime surface the two photons will correspond to spiraling lines separated by precicely one lap. Clearly the photons will reach the center dip still separated by one lap - meaning that the inside observer experiences only a 5 second time difference between the photons. This means that a person standing inside the planet and looking at a good clock somewhere outside the planet will see the clock ticking twice as fast as his own - in fact everything on the outside will appear to happen very fast. Conversely, a person on the outside will see everything inside the planet evolving very slowly.

Question

Suppose that you live outside the planet in question and you have an exam in three days - but you are already fully expert on the subject - and you would like to take the exam as soon as possible (this is obviously a very common problem among students:). Knowing the shape of spacetime, is there a way to arrange that?

Comments

There is much more to say about this illustration - and many more similar illustrations of for instance black holes and Big Bang spacetimes. For the moment the above illustration will however have to suffice.